 Fibonnacci’s
Sequence
Fibonnacci’s
Sequence
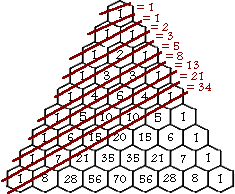
By looking
at the triangle above, you can see some rows cutting the Pascal's Triangle,
but when you add up the numbers between two consecutive rows, you can find
that it equals to the number next to the equal sign beside the triangle.
All this number 1, 1, 2, 3, 5, 8, 13, 21, we called it ‘Fibonnacci’s Sequence’.
This sequence can be formed by adding 2 consecutive numbers in the sequence
to produce the next number. This sequence can be found in many places such
as length of the segments of a pentagram etc.
<U>
 Back
to home
Opdateret d. 26/3/00
Back
to home
Opdateret d. 26/3/00
